-
擅长：
标准差/平均值*100%9人赞同 2018-09-23发表于 -
平均值、标准差、变异系数的计算(1)
平均值、标准差、变异系数的计算(1)
391.6 0.26 506.3 0.20 578.5 0.18 394 0.26 732.4 0.14 412.5 0.25 373.4 0.27 766.4 0.13 475.9 0.21 619.2 0.16 515.6 0.20 501.1 0.20 352.6 0.29 434.8 0.23 377.4 0.27 290.5 0.35 531.1 0.19 399.9 0.25 419.6 0.24 407.9 0.25 506.8 0.20 559.5 0.18 535.2 0.19 395.5 0.26 506.1 0.20 282.1 0.36 488.6 0.21 523.9 0.19 518.9 0.20 326.1 0.31 340 0.30 478.6 0.21 402 0.25 552.4 0.18 313.9 0.32 591 0.17 384.4 0.26 5
平均值、标准差、变异系数的计算
平均值、标准差、变异系数的计算
统计个数 6 6 6 6 6 6 最大值 15.8 6 6 30.5 17.4 13.2 最小值 6 2.14 0.389 6 6 6 平均值 13.32 2.18 0.43 29.38 17.08 12.30 标准差 2.23 0.02 0.04 0.82 0.38 0.61 变异系数 0.17 0.01 0.08 0.03 0.02 0.05 2.45 2.45 2.45 2.45 2.45 2.45 36.00 36.00 36.00 36.00 36.00 36.00 0.70 0.70 0.70 0.70 0.70 0.70 0.13 0.13 0.13 0.13 0.13 0.13 0.14 0.01 0.07 0.02 0.02 0.04 统计修正系数 0.86 0.99 0.93 0.98 0.98 0.96 标准值 11.47 2.16 0.40 28.70 16.77
-
擅长：
CV变异系数的公式：
(标准偏差SD、平均值MN)
标准差与平均数的比值称为变异系数，记为C.V(Coefficient of Variance)。
用公式表示为：CV=σ/μ。
意义：当需要比较两组数据离散程度大小的时候，如果两组数据的测量尺度相差太大，或者数据量纲的不同，直接使用标准差来进行比较不合适，此时就应当消除测量尺度和量纲的影响，而变异系数可以做到这一点，他是标准差与其平均数的比。CV虽然没有量纲，同时又按照其均数大小进行了标准化，这样就可以进行客观比较了。因此，可以认为变异系数和极差、标准差和方差一样，都是反映数据离散程度的绝对值。其数据大小不仅受变量值离散程度的影响，而且还受变量值平均水平大小的影响。
5人赞同 2018-09-23发表于 -
擅长：
CV变异系数的公式：
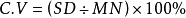
(标准偏差SD、平均值MN)
标准差与平均数的比值称为变异系数，记为C.V(Coefficient of Variance)。
用公式表示为：CV=σ/μ。
67人赞同 2018-09-24发表于
