结构的失稳现象可分为两类。图4所示的失稳现象,常称为丧失第一类稳定性,或称为分支点失稳。例如图4(a)所示的悬臂杆,当F1Cr时,仅有与承受轴向压力相应的轴向变形产生;但当F2=FCr时[见图4(b)],除产生与受压相应的轴向变形外,还将产生与受弯相应的弯曲变形。因此,在内力和变形的性质上都起了质变。
第一类稳定性也可以这样来进行描述:当FCr时,悬臂杆一直保持只受轴力的直线平衡形式[见图3(a)];当F=FCr时,出现了平衡分支现象,即悬臂杆既可以保持原来只受轴力的直线平衡形式,也可以有一个新的不定幅值的同时受压和受弯的弯曲平衡形式[见图4(b)],其中,ymax为悬臂杆的顶点水平位移。这一特性标志着当F=FCr时出现了临界平衡状态,它是处在由稳定平衡向不稳定平衡过渡的临界点上。
丧失第一类稳定的现象,在其他结构中同样也可出现。例如,图5(a)所示为在静水压力作用下处于轴心受压状态的圆拱。当水压力q小于其临界值qCr时,它维持圆形的平衡形式。当q达到qCr时,这种变形形式就成为不稳定的,由于某种扰动,即可能出现一种新的类似波浪形的变形形式,如图5中虚线所示。对于图5(b)所示的平面刚架,当荷载FCr时,刚架柱处于轴心受压状态而只有压缩变形;当荷载F=FCr时,刚架原来的平衡状态变成不稳定的,由于某种扰动,即将出现如图5中虚线所示的变形形式。由上可知,对于丧失轴心受压的稳定,其特点是体系的变形形式发生质的变化,出现了具有压缩和弯曲两种变形的形式。
图6(a)所示的薄壁工字梁,当荷载FCr时,梁在荷载作用的竖向平面内发生弯曲变形,即保持平面弯曲的平衡形式。当荷载F=FCr时,平面弯曲形式的平衡成为不稳定的,此时梁可能出现一种新的平衡形式:梁将偏离原来荷载作用的平面而发生斜弯曲和扭转,如图6中实线所示,即丧失了平面弯曲形式的稳定。再如承受静水压力作用的圆环[见图6(b)],当荷载q未抵达临界值qCr前,结构中仅承受轴向压力,将保持原有结构形状上的稳定平衡,当荷载q抵达临界值qCr时,原有结构的平衡形式将成为不稳定的,将出现如图6中虚线所示的平衡形式。
综上所述可知,丧失第一类稳定性的特征:结构的变形产生了性质上的突变。即原来的平衡形式成为不稳定的,而可能出现新的与原来平衡形式有质的区别的平衡形式,同时,这种现象是带有突然性的。
除上述丧失第一类稳定性的情况外,尚有丧失第二类稳定性的情况,这是两种性质不一样的稳定性概念。这类丧失稳定的特征是结构原来的变形将大大发展,而不会出现新的变形形式。即结构的平衡形式并不发生质变,但由于变形的增大,结构将不能正常工作。例如,图7(a)所示为两端铰支承受偏心压力F的直杆,当杆件开始受力时即同时处于受压和受弯状态,并伴生了挠度。荷载与挠度之间的关系如图8所示。当FCr时,若不继续增大荷载,则杆件的挠度也不增加。但当F值抵达FCr后,即使不再继续增加荷载甚至减小荷载,挠度仍将继续增大,称这种现象为丧失第二类稳定性。加载至极值点A时的荷载值FCr即为丧失第二类稳定性的临界荷载。因此,又把丧失第二类稳定性称为极值点失稳,显然,它与丧失第一类稳定性相比具有不同的概念。图7(b)所示为承受横向荷载F1(假定F1保持常量)同时承受压力F作用的压弯杆件,失稳时也有类似于偏心压杆的特征。
综上所述,丧失第二类稳定性的特点为:平衡形式并不发生质的变化,随着荷载F的逐渐增加,变形仅以量变的形式迅速增长,最后使结构丧失承载能力。
丧失第二类稳定性时的临界值实际上要低于丧失第一类稳定性时的临界值,这是因为杆件在偏心受压或压弯的情况下,随着荷载F的不断增加,截面的边缘纤维应力将首先抵达屈服极限,引起局部的塑性变形,使截面进入弹塑性阶段的工作状态,而塑性变形扩展的结果,就导致杆件承载能力的降低。
作用于结构上的荷载,一般并非都使杆件产生轴向受压,例如,受压弯作用的刚架柱、压力曲线不与拱轴相重合的各类拱结构、非理想桁架中的某些杆件等。因此,工程中的稳定问题实际上均属于第二类稳定性问题。研究第二类稳定性要涉及多种因素的影响,首先荷载一位移关系是几何非线性的,其次有时还要考虑到材料的非线性性质。因此,它比第一类稳定要复杂得多。为了计算简便起见,可针对结构的荷载作用方式作某些简化假定,将第二类稳定化为第一类稳定来处理,并通过某些系数反映两类稳定问题之间的差别。
对于工程结构来说,丧失上述两类稳定性都是不能允许的。 2100433B

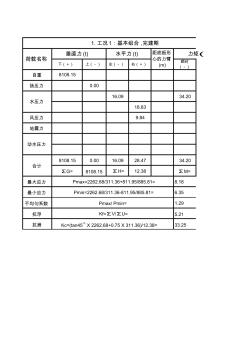 泵房稳定计算 (2)
泵房稳定计算 (2)

 渗流稳定计算
渗流稳定计算